Glinka method
In: Notch effect
The Glinka method allows a conversion of fictitious wholly elastic stress values obtained from a FEM to “real” elastic-plastic values. It is in close relation to Neuber method (here more information can be found). It relates the equivalent strain energy density for both states – the elastic fictitious one as well the real elastic-plastic one:
![]()
The equality thus has a bit more of physical foundation in comparison to Neuber method.
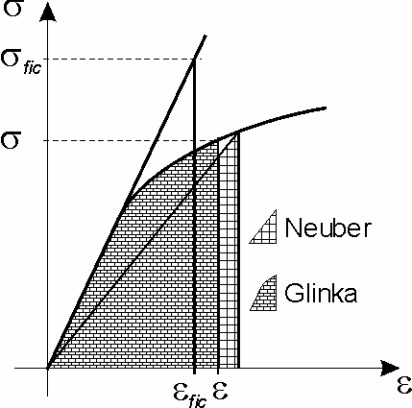
The integration utilizing Ramberg-Osgood relation of the cyclic stress-strain curve than gives:
![]() ,
,
which in turn can be rewritten to:
![]() ,
,
if the parameters of the Basquin-Manson-Coffin curve are used. This is the form implemented in PragTic. The unknown stress parameter is retrieved by Newton-Raphson iterative method.
The method is usable for uniaxial calculations only, since it relates scalar values.
Nomenclature:
|
Mark |
Unit |
PragTic variable |
Meaning |
|
b |
[-] |
EXP_B |
fatigue strength exponent |
|
c |
[-] |
EXP_C |
fatigue ductility exponent |
|
E |
[MPa] |
E |
elastic modulus |
|
|
[-] |
|
strain |
|
|
[-] |
EPS_F |
fatigue ductility coefficient |
|
K’ |
[MPa] |
K’ |
cyclic hardening coefficient |
|
n’ |
[-] |
N’ |
cyclic hardening exponent |
|
|
[MPa] |
|
stress |
|
|
[MPa] |
SIG_F |
fatigue strength coefficient |
|
|
|
|
|
|
|
|
|
fictitious elastic value of x retrieved from a linear FE-computation |
More:
local elastic-plastic strain analysis
© PragTic, 2007
This help file has been generated by the freeware version of HelpNDoc